This post is brought to you by RJMetrics. We provide hosted business intelligence software that helps web-based businesses harness the power of their data to make smarter business decisions. Check us out!
The Experiment
With the increased use of sports analytics and this year’s NBA finals, I thought it would be interesting to construct a rudimentary model projecting the outcome of the 2010 NBA Finals.
To gather data, I referenced the NBA Encyclopedia – Playoff Edition from NBA.com. I aggregated data points containing year, game number, home/away teams, home/away scores from all Finals games since 1946 (363 games).
These data points were fed into a model which ran 10,000 Monte Carlo simulations of the NBA finals. We can use the results of these simulations to draw insights about the outcome of the series.
Some highlights:
- In 64% of the simulations, the Lakers won the series
- The most likely outcome was a Lakers sweep, representing 11% of the simulations
- The probability of a 7-game series was 29%
- Given the current state of the series (Lakers up 2-1), the numbers heavily suggest a Lakers win:
- The chance of the Celtics winning the championship in any number of games is now just 25%
- The most likely outcome is Lakers in 7 games (31%)
- The next most likely outcomes Lakers in 5 games (22%) and Lakers in 6 games (21%)
The Results
After collecting the necessary data, I calculated three key statistics: home court winning percentage by game number, “streaking” momentum probability, and a weighted expected winning percentage based on the regular season stats.
These stats are obviously not fully independent, nor do they represent perfectly clean input data (for example, which teams played “home” in which games has changed during the NBA’s history). However, they each provided some interesting insights into the historical outcome of NBA Finals match-ups.
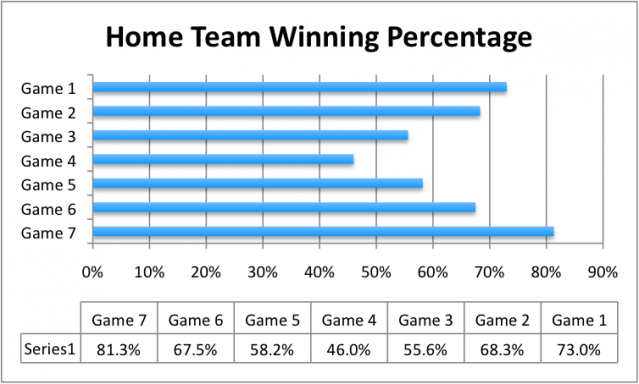
The historical home team winning percentage by game is shown below.
Throughout the life of the NBA, games 3 and 4 have been played at the home of the team with the worse regular-season record. The impact of regular season records is evident in the dip seen during those games in the chart above.
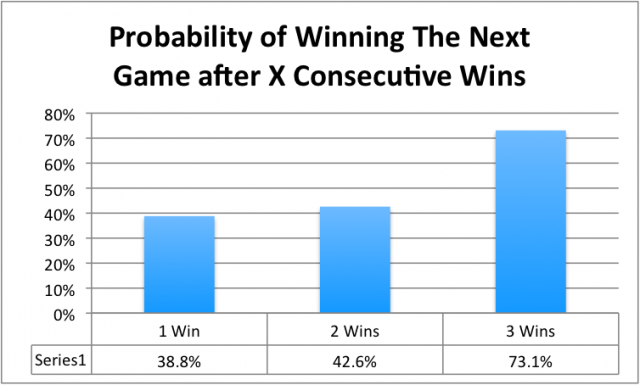
The propensity to have a winning streak is also interesting:
As you might expect, with each consecutive win your chances of winning the next game go up. However, what I found very interesting is how low the historical chances are of winning a second game in a row. I have a few theories on what might be influencing that statistic:
- The Finals highlight the two most competitive teams so there is likely to be less dominance between the teams. This makes you less likely to see a multi-game winning streak in finals play than it is to see some back-and-forth between teams.
- Factors such as home court advantage could be influencing the numbers, as the “home” team switches often throughout the series.
My final statistic was a simple weighted average of the two teams’ regular season winning records. I used this as a baseline probability that the Lakers would win any given game in the series (53.3%).
To simulate the games in the series, I took each of these three inputs and weighted them equally in a 10,000 iteration Monte Carlo simulation of the series. There are obviously countless other ways I could have approached the problem or chosen to weigh these statistics. I chose this rudimentary “equal weighting” methodology to provide some basic insights into how my inputs would combine to create simulated outcomes.
After running the simulations, the following statistics surfaced:
From beginning of NBA Finals:
- Probability Lakers win series: 64%
- Probability Celtics win series: 36%
- Most likely game-by-game series outcome: A Lakers sweep (11% chance)
- The next four most likely series outcomes were the four permutations of a Lakers Championship in 5 games (these, combined with the previous stat, meant a 26% chance of the Lakers winning inf 5 games or less).
- Least likely series outcome: C-C-C-L-L-L-C
- Expected length of series: 5.8 games
Given what has occurred through 3 games of the NBA Finals (with the Lakers up 2-1 as of Tuesday night):
- Probability Lakers win series: 75%
- Probability Celtics win series: 25%
- Most likely series outcome: L-C-L-L-C-L (Lakers in 6)
- Least likely series outcome: L-C-L-L-C-C-C (Celtics in 7)
- Expected length of series: 6.2 games
Here are the chances of each possible remaining outcome:
- Lakers in 7: 31%
- Lakers in 5: 22%
- Lakers in 6: 21%
- Celtics in 7: 15%
- Celtics in 6: 10%
Interestingly, even if the Celtics win game 4 (tying the series 2-2), the Lakers are still more favored than they were before the series started (60% vs 53%).
The Methodology
I found the process of extracting and analyzing the data to be quite educational. If you’re curious about how I arrived at these numbers, read on.
Game-by-Game Home Court Advantage Explained
To create the game-by-game home court advantage for the Finals, I used all data points since the NBA finals began in 1946. The data points were simply the percentage of “home court wins” across the entire data set by game number.
For those of you familiar with the NBA Finals format, you may know that the format changed from 2-2-1-1-1 to 2-3-2 after the 1984 finals. This means that games 1,2,6,7 have been played at the superior team’s home court for the past 25 years. Prior to 1985, the 2-2-1-1-1 Finals format held steady with a few exceptions.
The older series format held games 1,2,5,7 at the superior team’s home court from 1946-1984 (39 years). I initially wanted to just use the newer playoff format to avoid an inflation in the game 5 home winning percentage (from game 5 being held at the superior team home court for 39 years) and to avoid deflation in the game 6 home winning percentage (from game 6 being held at the inferior team home court for 39 years). However, to achieve a statistically significant amount of data points in all situations, I aggregated the two playoff formats and took all 64 years of Finals data.
Momentum Analysis Explained
Every game that is played (except for the first in the series) is an opportunity to continue a streak. Streaks can be as short as two games and as long as four (since, after winning four games, the series has ended). Streaks also end organically when the series ends, so we have to be careful to not count “end of series” games as missed opportunities to continue streaks.
A 4 game sweep (as LA accomplished in this year’s Utah series) is viewed as and limited strictly to 3 statistical data points in our momentum analysis
- Given one win, what was the outcome of the second game?
- In this case, the result is a successful conversion of a 1 game streak into a 2 game streak
- Given two consecutive wins, what was the outcome of the third game?
- In this case, the result is a successful conversion of a 2 game streak into a 3 game streak
- Given three consecutive wins, what was the outcome of the fourth game?
- In this case, the result is a successful conversion of a 3 game streak into a 4 game streak
Note that we do not count mini-streaks within a streak as their own streaks (for example, the third win in a 3-game streak doesn’t also count as the second win in a two-game streak).
We chose to exclusively use historical Finals data for “streakiness.” We considered using 2009-2010 regular season data for Lakers and Boston streakiness but decided against it for two reasons.
- There were not enough data points from the regular season to provide a good basis for analysis
- The characteristics of a “streak” in the regular season are quite different, as they can span different teams and stretch far beyond the “4 game” limit of a playoff series.
Head to Head Winning Percentage Explained
To create the head to head winning percentages, I simply looked at each team’s regular season winning percentages (50-32 and 57-25) and determined that the winning percentage of the Lakers was 14% larger than that of the Celtics.
I then constructed a head-to-head winning probability for the Lakers that was 14% better than the complimentary winning probability of the Celtics.
Conclusion
I hope you enjoyed learning about my experience simulating the NBA finals using statistics. There are obviously a number of areas where this model could be expanded and improved, and I hope to explore them in the future.
Thanks to RJMetrics for supporting this small project as part of my summer internship. If your web-based business needs better insight into its backend data, RJMetrics can help you measure, manage, and monetize better. Give it a try!